Question

A corporation randomly selects 150 salespeople and finds that 66% who have never taken a self- improvement course would like to do so. The firm did a similar study 10 years ago and found that 70% of a random sample of 160 salespeople wanted a self-improvement course. The groups are assumed to be independent random samples. Let π1 and π2 represent the true proportion of workers who would like to attend a self-improvement course in the recent study and the past study, respectively.What is the value of the χ2 test statistic to use in evaluating the alternative hypothesis that there is a difference in the two population proportions using α = 0.05?

Answer 1

We conclude that there is no difference in the two population proportions using α = 0.05.

Explanation:

We are given that a corporation randomly selects 150 salespeople and finds that 66% who have never taken a self- improvement course would like to do so.

The firm did a similar study 10 years ago and found that 70% of a random sample of 160 salespeople wanted a self-improvement course.

Let
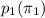`p_1 (\pi_1)` = true proportion of workers who would like to attend a self-improvement course in the recent study.

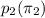`p_2 (\pi_2)` = true proportion of workers who would like to attend a self-improvement course in the past study.

SO, Null Hypothesis,
`H_0` :
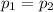`p_1=p_2` {means that there is no difference in the two population proportions}

Alternate Hypothesis,
`H_A` :
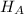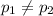`p_1\\eq p_2` {means that there is a difference in the two population proportions}

The test statistics that would be used here Two-sample z test for proportions;

T.S. =
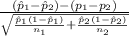`\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{(\hat p_1(1-\hat p_1))/(n_1)+(\hat p_2(1-\hat p_2))/(n_2) } }` ~ N(0,1)

where,
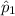`\hat p_1` = sample proportion of salespeople who would like to attend a self-improvement course in recent study = 66%

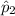`\hat p_2` = sample proportion of salespeople who would like to attend a self-improvement course in past study = 70%

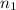`n_1` = sample of salespeople in recent study = 150

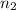`n_2` = sample of salespeople in past study = 160

So, the test statistics =
`\frac{(0.66-0.70)-(0)}{\sqrt{(0.66(1-0.66))/(150)+(0.70(1-0.70))/(160) } }`

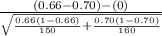
= -0.755

The value of z test statistics is -0.755.

Now, at 0.05 significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.

Since our test statistic lies within the range of critical values of z, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that there is no difference in the two population proportions.