Answer:
(a) The proportion of people using nicotine gum that stopped smoking is 0.12 and the proportion of people using the placebo that stopped smoking is 0.05.
(b) The value of z test statistics is 7.242.
Explanation:
We are given that a study used nicotine gum to help people quit smoking. The study was placebo-controlled, randomized, and double-blind.
The results showed that 197 out of 1647 people using the nicotine gum succeeded, and 85 out of 1620 using the placebo succeeded.
Let
 = population proportion of people who quit smoking using nicotine gum.
= population proportion of people who quit smoking using nicotine gum.
 = population proportion of people who quit smoking using placebo.
= population proportion of people who quit smoking using placebo.
SO, Null Hypothesis,
 :
:
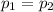
Alternate Hypothesis,
 :
:
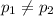
The test statistics that would be used here Two-sample z test for proportions;
T.S. =
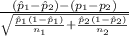 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of people using nicotine gum that stopped smoking =
= sample proportion of people using nicotine gum that stopped smoking =
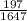 = 0.12
= 0.12
 = sample proportion of people using placebo that stopped smoking =
= sample proportion of people using placebo that stopped smoking =
 = 0.05
= 0.05
 = sample of people using the nicotine gum = 1647
= sample of people using the nicotine gum = 1647
 = sample of people using the placebo = 1620
= sample of people using the placebo = 1620
So, the test statistics =
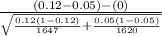
= 7.242
The value of z test statistics is 7.242.