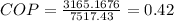Question

An ideal Brayton cycle refrigeration cycle has a compressor pressure ratio of 6. At the compressor inlet, the pressure and temperature of the entering air are 20 lbf/in2 and 460 R. The temperature at the inlet of the turbine is 700 R. For a refrigerating capacity of 15 tons, determine (a) the mass flow rate in lbm/min. (b) the net power input, in Btu/lbm. (c) the coefficient of performance."

Answer 1

(a) 185.1002 lbm/min

(b) 7125.12 Btu/min

(c) 0.42

Step-by-step explanation:

Here we have;

`(T_2)/(T_1) = (T_4)/(T_3)=\left ((p_(2))/(p_(1)) \right )^{(\gamma -1)/(\gamma )}`

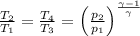
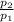`(p_(2))/(p_(1))` = 6

γ = 1.4 for air

T₁ = 460 R = 255.56 K

T₃ = 700 R = 388.89 K

1 ton of refrigeration capacity = 3.52 kWh = 0.98 W

∴ 15 ton = 15×3.52 = 52.8 kW/h

= 189910.0534716 kJ/h = 3165.1676 kJ/min

`\therefore (T_2)/(460) = \left 6\right ^{(1.4 -1)/(1.4 )} = 1.669`

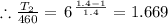
T₂ = 1.669 × 460 = 767.515 R = 426.4 K

Refrigeration effect per kg = 1 ×
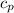`c_p` × (T₃ - T₂) = 1.005 × (700 - 767.515) = 67.85 = 37.7 kJ/kg

`Mass \, of \, air \, circulated = (Refrigeration \ effect)/(Refrigeration \ effect \, per \, kg)`

`Mass \, of \, air \, circulated \ per \ minute = (3165.1676 )/(37.7 ) = 83.96 \, kg/min`

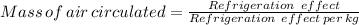
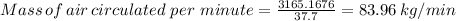
83.96 kg/min = 185.1002 lbm/min

(b)
`W_(comp) = (\gamma)/(\gamma -1) mR(T_4 - T_3)`

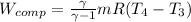
T₄ = T₃×1.669 = 700×1.669 = 1167.96 °R = 648.9 K

`= (1.4)/(1.4 -1) * 83.96 * 0.287 * (648.9 - 388.89)`

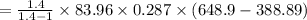
= 21925.83 kJ/min

`W_(exp) = (\gamma)/(\gamma -1) mR(T_1 - T_2)`

`= (1.4)/(1.4 -1) * 83.96 * 0.287 * (426.4 - 255.56)`

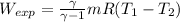
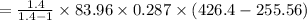
= 14408.4 kJ/min

`W_(cycle) = W_(comp) - W_(exp)`

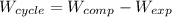
= 21925.83 - 14408.4 = 7517.43 kJ/min

`Power \, required= (7517.43)/(60) \, kJ/s = 125.29 \, kW`

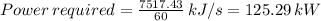
1 kW = 56.87 Btu/min

Therefore;

125.29 kW = 7125.12 Btu/min

(c) The coefficient of performance (COP), is given by the relation;

`COP = (3165.1676 )/(7517.43) = 0.42`