Question

When a survey asked subjects whether they would be willing to accept cuts in their standard of living to protect the​ environment, 352352 of 11951195 subjects said yes. a. Find the point estimate of the proportion of the population who would answer yes. b. Find the margin of error for a​ 95% confidence interval. c. Construct the​ 95% confidence interval for the population proportion. What do the numbers in this interval​ represent? d. State and check the assumptions needed for the interval in ​(c) to be valid.

Answer 1

(a) The point estimate of the proportion of the population who would answer yes is 0.295.

(b) The margin of error for a​ 95% confidence interval is 0.0259.

(c) 95% confidence interval for population proportion is [0.2691 , 0.3209].

Explanation:

We are given that a survey asked subjects whether they would be willing to accept cuts in their standard of living to protect the​ environment, 352 of 1195 subjects said yes.

Let
`\hat p` = sample proportion of subjects who said yes.

(a) The point estimate of the proportion of the population who would answer yes =
`\hat p` =
`(X)/(n)`

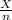
So,
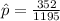`\hat p = (352)/(1195)` = 0.295

(b) Margin of error is given by =
`Z_(_(\alpha)/(2)_) * \text{Standard of Error}`

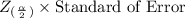
where,
`\alpha` = level of significance = 1 - 0.95 = 5%

At 5% level of significance, z table gives critical value of 1.96 for two-sided interval.

Standard of error =
`\sqrt{(\hat p(1-\hat p))/(n) }` =
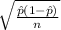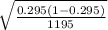`\sqrt{(0.295(1-0.295))/(1195) }` = 0.0132

So, Margin of error for 95% confidence interval =
`1.96 * 0.0132`

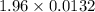
= 0.0259

(c) 95% confidence interval for population proportion is given by =

Point estimate
`\pm` Margin of error

⇒ 0.295
`\pm` 0.0259

⇒ [0.295 - 0.0259 , 0.295 + 0.0259]

⇒ [0.2691 , 0.3209]

So, 95% confidence interval = [0.2691 , 0.3209]

The numbers in this interval​ represent that we are 95% confident that the population proportion will lie between 0.2691 and 0.3209.

(d) Assumptions needed for constructing a confidence interval are;

• The data must be sampled randomly.
• Sample values must be independent of each other.
• Data must follow normal distribution.