Question

g Visible light travels in air, which has an index of refraction of 1.0. It is incident on plastic which is covered by a coating (such that light hits the coating before the plastic). The coating has an index of refraction of 1.6 and is 0.50 microns thick. The ray reflected off the air-coating interface and the ray reflected off the coating-plastic interface experience interference. What frequencies could the light be

Answer 1

The interference is constructive. The plastic used has an index of refraction of 1.7

Step-by-step explanation:

Given that :

Visible light travels in air, which has an index of refraction of 1.0

i.e
`\mathbf{n_(air) = 1.0}`

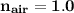
The coating has an index of refraction of 1.6

i.e
`\mathbf{n_(coat) = 1.6}`

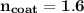
Since the index of refraction of air is incident on the plastic which is covered by a coating ; then
`\mathbf{n_(plastic) = 1.7}`

Now; for constructive interference:

`\mathbf{2 nt_(coat) =m \lambda _ m}`

`\mathbf{\lambda _ m =(2 nt_(coat))/(m) }`

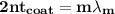
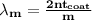
where ;

m =1, 2, ... n

For m = 1

`\mathbf{\lambda _ 1 =(2 *1.6*0.50*10^(-6))/(1) }`

`\mathbf{\lambda _ 1 =1.6*10^(-6) \ m}`

`\mathbf{f_1 =(c)/(\lambda_1) }`

`\mathbf{f_1} =(3*10^8)/(1.6*10^(-6) )`

`\mathbf{f_1 =1.875*10^(14) \ Hz}`

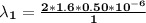
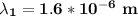
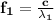
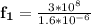
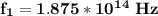
For m =2

`\mathbf{\lambda _ 2 =(2 *1.6*0.50*10^(-6))/(2) }`

`\mathbf{\lambda _ 1 =8.0*10^(-7)m}`

`\mathbf{f_2 =(c)/(\lambda_2) }`

`\mathbf{f_2} =(3*10^8)/(8*10^(-7) )`

`\mathbf{f_2 =3.75*10^(14) \ Hz}`

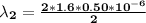
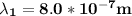
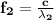
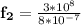
`\mathbf{f_n=n(1.875)*10^(14) \ Hz}` for n = 1, 2 , .......