Question

A nationwide survey of college seniors by a university revealed that almost 70​% disapprove daily pot​ smoking, according to a report in a magazine. If 14 seniors are selected at random and asked their​ opinion, find the probability that the number who disapprove of smoking pot daily is​ (a) anywhere from 7 to 9​, ​(b) at most 5 and​ (c) not less than 8.

Answer 1

a) P ( 7 ≤ X ≤ 9) = 0.384

b) P(X ≤ 5) = 0.0083

c) P( X ≥ 8) = 0.904

Explanation:

Proportion of college seniors that disapprove daily pot smoking, p = 0.7

Proportion of college seniors that do not disapprove daily pot smoking,

q = 1 - p = 1 - 0.7

q = 0.3

14 seniors are selected i.e. sample size, n = 14

This is a binomial distribution question:

`p(X = r) = nCr p^(r) q^(n-r)`

a) probability that the number who disapprove of smoking pot daily is anywhere from 7 to 9​

P ( 7 ≤ X ≤ 9) = P(X=7) + P(X=8) + P(X=9)

`P(X=7) = 14C7 p^(7) q^(14-7) \\P(X=7) = 14C7 * 0.7^(7) 0.3^(7)\\P(X=7) = 3432 * 0.7^(7) 0.3^(7)\\P(X=7) = 0.062`

`P(X=8) = 14C8 p^(8) q^(14-8) \\P(X=8) = 14C8 * 0.7^(8) 0.3^(6)\\P(X=8) = 3003 * 0.7^(8) 0.3^(6)\\P(X=8) = 0.126`

`P(X=9) = 14C9 p^(9) q^(14-9) \\P(X=9) = 14C9 * 0.7^(9) 0.3^(5)\\P(X=9) = 2002 * 0.7^(9) 0.3^(5)\\P(X=9) = 0.196`

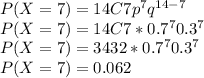
P ( 7 ≤ X ≤ 9) = P(X=7) + P(X=8) + P(X=9)

P ( 7 ≤ X ≤ 9) = 0.062 + 0.126 + 0.196

P ( 7 ≤ X ≤ 9) = 0.384

b) Probability that the number who disapprove of smoking pot daily is​ at most 5

P(X ≤ 5) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)

`P(X=0) = 14C0 p^(0) q^(14-0) \\P(X=0) = 14C0 * 0.7^(0) 0.3^(14)\\P(X=0) = 1 * 0.7^(0) 0.3^(14)\\P(X=0) = 0.0000000478`

`P(X=1) = 14C1 p^(1) q^(14-1) \\P(X=1) = 14C1 * 0.7^(1) 0.3^(13)\\P(X=1) = 14 * 0.7^(1) 0.3^(13)\\P(X=1) = 0.00000156`

`P(X=2) = 14C2 p^(2) q^(14-2) \\P(X=2) = 14C2 * 0.7^(2) 0.3^(12)\\P(X=2) = 91 * 0.7^(2) 0.3^(12)\\P(X=2) = 0.0000237`

`P(X=3) = 14C3 p^(3) q^(14-3) \\P(X=3) = 14C3 * 0.7^(3) 0.3^(11)\\P(X=3) = 364 * 0.7^(3) 0.3^(11)\\P(X=3) = 0.000221`

`P(X=4) = 14C4 p^(4) q^(14-4) \\P(X=4) = 14C4 * 0.7^(4) 0.3^(10)\\P(X=4) = 1001 * 0.7^(4) 0.3^(10)\\P(X=4) = 0.00142`

`P(X=5) = 14C5 p^(5) q^(14-5) \\P(X=5) = 14C5 * 0.7^(5) 0.3^(9)\\P(X=5) = 2002 * 0.7^(5) 0.3^(9)\\P(X=5) = 0.00662`

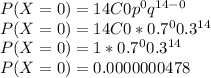
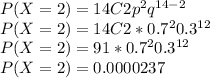
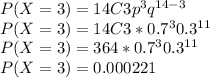
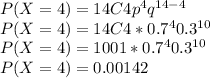
P(X ≤ 5) = 0.0000000478 + 0.00000156 + 0.0000237 + 0.000221 + 0.00142 + 0.00662

P(X ≤ 5) = 0.0083

c) Probability that the number who disapprove of smoking pot daily is​ not less than 8.

P( X ≥ 8) = P(X=8) + P(X=9) + P(X=10) + P(X=11) + P(X=12) + P(X=13) + P(X=14)

`P(X\geq 8) = (14C8 * 0.7^(8) 0.3^(6)) + (14C9 * 0.7^(9) 0.3^(5)) + (14C10 * 0.7^(10) 0.3^(4)) + (14C11 * 0.7^(11) 0.3^(3)) + (14C12 * 0.7^(12) 0.3^(2)) + ( 14C13 * 0.7^(13) 0.3^(1)) + (14C14 * 0.7^(14) 0.3^(0))`

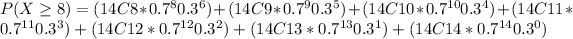
P( X ≥ 8) = 0.126 + 0.194 + 0.229 + 0.194 + 0.113 + 0.041 + 0.00678

P( X ≥ 8) = 0.904