The missing part of the question is show in bold format.
Your teacher gives you a number cube with numbers 1-6 on its faces. You are asked to state a theoretical probability model for rolling it
once. Your probability model shows a probable outcome of 1/6 for each of the numbers on the cube, 1 chance for all any of the 6 numbers.
You roll it 500 times and get the following data:
Outcome 1 2 3 4 5 6
Frequency 77 92 75 90 76 90
Exercises 1–2
1. If the equality model was correct, about how many of each outcome
would you expect to see if the cube is rolled 500 times
2. Based on the data from the 500 rolls, how often were odd numbers observed? How often were even numbers observed?
Answer:
Explanation:
1.
If the equally likely model was correct, about how many of each outcome
would you expect to see if the cube is rolled 500 times.
The probability of rolling any of the numbers from 1 to 6 is p(1/6)
The number of each of the outcomes expected to be seen in 500 rolls of the number cube is
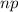
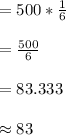
2. From the given data in the roll;
The odd numbers 1, 3 and 5, were obtained at 77, 75 and 76 times respectively.
Thus, the total number of times odd number were rolled = 77 + 75 + 76 = 228
Probability of an odd number turning up =
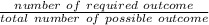
=
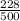
= 0.456
= 45.6%
The even numbers, 2, 4 and 6, were obtained 92, 90 and 90 times respectively.
The total number of times even number were rolled = 92 + 90 + 90 = 272
Probability of an even number turning up =
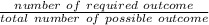
=
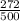
= 0.544
= 54.4%