Answer:
4
Explanation:
Given:
Number of cards = 52
Let probability of match, p =
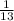
Let X follow a binomial distribution.
Thus,
X ~ B
![[52, (1)/(13)]](https://img.qammunity.org/2021/formulas/mathematics/college/ujkfm72xclq6zlufsx3a4q25r7pukb80md.png)
To compute the expected number of matches that occur would be:
![E(X) = np= 52[(1)/(13)]](https://img.qammunity.org/2021/formulas/mathematics/college/yoy5s9mv15l6r340zpzb7v8c062nglx6j1.png)
Solving further, we have:
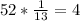
Therefore, the expected number of matches that occur is 4.