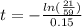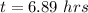Complete Question
The complete question is shown on the first uploaded image
Answer:
The time taken is
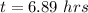
Step-by-step explanation:
From the question we are told that
The value of
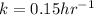
The the interior temperature is
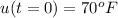
The external temperature is

The required interior temperature is
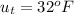
The newton cooling law is
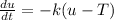
=>
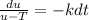
Now integrate both sides we have
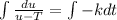
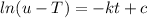
Since c is a constant lnC = c will also give a constant so

=>
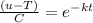
=>
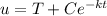
substituting value


Hence
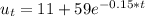
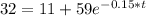
=>