Question

If x1 and x2 are the roots of equation x^2+5x−3, determine the value of x1^2 +x2^2

Answer 1

31

Explanation:

To find this solution to this problem, we first need to find the roots of the given equation, then we can square them to find our answers.

We are given the equation
`x^2+5x-3`

The first thing that we can do is check whether or not this quadratic equation is easily factorable. In this case, we are looking for two numbers that multiply to give -3 and add together to give 5. No whole numbers do this, so we must use the quadratic formula, which gives us the roots

The quadratic formula says
`(-b+√(b^2-4ac) )/(2a) ,(-b-√(b^2-4ac) )/(2a)`

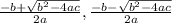
In the case of our quadratic equation,
`a=1, b=5, c=-3`

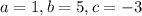
Now, we can plug these numbers into our formula and then simplify

`(-5+√((5)^2-4(-3)) )/(2(1))\\\\(-5+√(25+12) )/(2) \\\\(-5+√(37) )/(2) ,(-5-√(37) )/(2)`

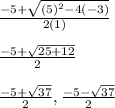
Now that we have the roots of this quadratic equation, all we need to do is square each of them

`((-5-√(37) )/(2) )^2\\\\(25+10√(37)+37 )/(4) \\\\(62+10√(37) )/(4) \\\\(31+5√(37) )/(2)`

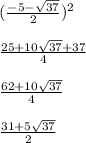
And now the second

`((-5+√(37) )/(2) )^2\\\\(25-10√(37)+37 )/(4) \\\\(62-10√(37) )/(4) \\\\(31-5√(37) )/(2)`

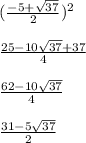
Lastly, we just need to add these roots together

`(31+5√(37) )/(2)+(31-5√(37) )/(2) \\\\(62)/(2) \\\\31`