Answer:
Explanation:
Hello!
Full text in attachment.
Given the data of the dependent variable Y and the independent variable X,
you have to estimate the linear regression: ^Y= a + bX
Where "a" is the estimate of the intercept and "b" is the estimate of the slope.
n= 9
∑X= 42.70; ∑X²= 250.45; ∑Y= 120.05; ∑Y²= 1801.03; ∑XY= 665.16
Y[bar]= 13.34; X[bar]= 4.74
Using the software I've calculated the asked values:
The slope of the line is
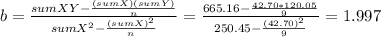
The value of the Y-intercept is a= Y[bar] -bX[bar]= 13.34-1.997*4.74= 3.86
The standard error of the slope is Sb= 0.16
The standard error of the Y-intercept is Sa= 0.86
The degrees of freedom for the hypothesis test for the slope (t-test) are n-2= 9-2= 7
The SSresidues= 8.81
I hope this helps!