Answer:
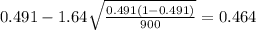

We are 90% confident that the true proportion of teenagers who have used at least one informal element in school writing assignments is between 0.464 and 0.518
Explanation:
We can begin finding the estimator for the proportion of interest:
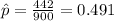
The confidence level is 90% , and the significance level would be given by
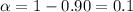 and
and
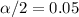 . And the critical value would be given by:
. And the critical value would be given by:
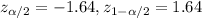
The confidence interval for the mean is given by the following formula:
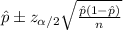
Replacing the info given we got:
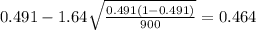

We are 90% confident that the true proportion of teenagers who have used at least one informal element in school writing assignments is between 0.464 and 0.518