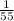Question

A bag contains tiles with the letters p -r-o-b-a-b-i-l-i-t-y Tyler chooses a tile without looking and doesn't replace it he chooses a second tile without looking what is the probability that he will choose the letter i both times

1/55
2/55
2/121
3/121

Answer 1

Multiply the fractions/probabilities

2 wanted tiles / 11 tiles in total x 1 wanted tile / 10 total tiles in total = 2/110 chance

2/110 = 1/55 chance

Hope this helps

Explanation:

Answer 2

`(1)/(55)`

Explanation:

Total number of tiles: 11 (obtained from counting the letters in probability)

Probability of picking the letter "i" the first time:

There are 2 letter "i's", and 11 total options, so the probability of picking an "i" is:

`(2)/(11)`

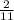
Probability of picking the letter "i" the second time:

We now have one less letter in the bag, as the first letter "i" was not replaced.

This means we now only have 1 letter "i", and 10 total options, so the probability of picking the last "i" is:

`(1)/(10)`

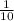
When you have two probabilities that are dependant on each other, you multiply them to get the probability of one, given that the other has happened.

Total probability:

`(2)/(11)*(1)/(10) = (2)/(110)`

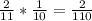
Simplify by dividing by 2:

`(1)/(55)`