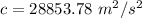Question

Where c is a constant that depends on the initial gas pressure behind the projectile. The initial position of the projectile is s=1.5m and the projectile is initially at rest. The projectile accelerates until it reaches the end of the barrel at s=3m. What is the value of the constant c such that the projectile leaves the barrel with a velocity of 200 m/s?

Answer 1

Complete Question

A gas gun uses high pressure gas tp accelerate projectile through the gun barrel.

If the acceleration of the projective is : a = c/s m/s​2

Where c is a constant that depends on the initial gas pressure behind the projectile. The initial position of the projectile is s= 1.5m and the projectile is initially at rest. The projectile accelerates until it reaches the end of the barrel at s=3m. What is the value of the constant c such that the projectile leaves the barrel with velocity of 200m/s?

Answer:

The value of the constant is
`c = 28853.78 \ m^2 /s^2`

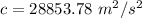
Step-by-step explanation:

From the question we are told that

The acceleration is
`a = (c)/(s)\ m/s^2`

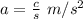
The initial position of the projectile is s= 1.5m

The final position of the projectile is
`s_f = 3 \ m`

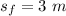
The velocity is
`v = 200 \ m/s`

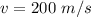
Generally
`time = (ds)/(dv)`

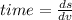
and acceleration is
`a = (v)/(time )`

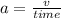
so

`a = v (dv)/(ds)`

=>
`vdv = a ds`

`vdv = (c)/(s) ds`

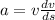
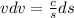
integrating both sides

`\int\limits^a_b vdv = \int\limits^c_d (c)/(s) ds`

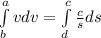
Now for the limit

a = 200 m/s

b = 0 m/s

c = s= 3 m

d =
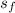`s_f`= 1.5 m

So we have

`\int\limits^(200)_(0) vdv = \int\limits^(3)_(1.5) (c)/(s) ds`

`[(v^2)/(2) ] \left | 200} \atop {0}} \right. = c [ln s]\left | 3} \atop {1.5}} \right.`

`(200^2)/(2) = c ln[(3)/(1.5) ]`

=>
`c = (20000)/(0.69315)`

`c = 28853.78 \ m^2 /s^2`