Question

Which of the quadratic functions has the narrowest graph?

Answer 1

`y=(1)/(8)x^2`

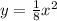
Explanation:

A quadratic function has the formula ax² + bx + c

• To determine if a graph will be narrow or wide, the leading coefficient, a, will be the factor that determines this
• The greater the coefficient, the narrower the parabola
• The lesser the coefficient, the wider the parabola

Here all of the functions are in the form ax²

• In
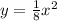  `y=(1)/(8)x^(2)`, our "a" term is
  `(1)/(8)`
• In y = -2x², our "a" term is -2
• In y = -3x², our "a" term is -3
• In
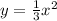  `y=(1)/(3)x^(2)`, our "a" term is
  `(1)/(3)`

We can eliminate the two functions with the negative coefficients because they are much smaller than the two functions with the fractions as coefficients, and will therefore open much wider.

We can now compare the two remaining functions,
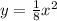`y=(1)/(8)x^2` and
`y=(1)/(3)x^2`

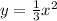
• Giving the two fractions common denominators would turn them into
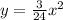  `y = (3)/(24)x^2` and
  `y=(8)/(24) x^2`
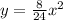
• The equation with the larger fraction will be the parabola that is the narrowest. In this case, it is the
  `y=(8)/(24) x^2`.
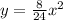• Therefore,
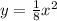  `y=(1)/(8)x^2` will have the narrowest graph