Question

In a survey of 1000 American adults conducted in April 2012, 43% reported having gone through an entire week without paying for anything in cash. Test to see if this sample provides evidence that the proportion of all American adults going a week without paying cash is greater than 40%. Use the fact that a randomization distribution is approximately normally distributed with a standard error of SE=0.016. Show all details of the test and use a 5% significance level.

1. State the null and alternative hypotheses.
2. What is the test statistic? Round your answer to two decimal places.
3. What is the p-value? Round your answer to two decimal places.
4. What is the conclusion?

Answer 1

1) H0 : p = 0.40

H1 : p > 0.40

2) 1.88

3) 0.030

4) Reject null hypothesis H0, since pvalue, 0.0301 is less than significance level, 0.05, and find evidence that the proprtion is greater than 40%.

Explanation:

Given:

Sample size, n = 1000

p = 40% = 0.40

p' = 43% = 0.43

S.E = 0.016

Significance level = 0.05

a) The null and alternative hypotheses.

H0 : p = 0.40

H1 : p > 0.40

b) Test statistic.

Let's take the Z formula:

`Z = (p' - p)/(SE)`

`Z = (0.43 - 0.40)/(0.016)`

`= (0.03)/(0.016) = 1.875`

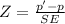
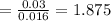
= 1.875 ≈ 1.88

The test statistic = 1.88

3) For the P-value, we have:

P(Z ≥ 1.88) = 0.0301 ≈ 0.030

P-value = 0.030

Critical value at 0.05 significance level for a right tailed test is 1.645

Decision: Reject null hypothesis H0, if p-value is less than significance level and if test statistic Z, is greater than critical value.

4) Conclusion: Reject null hypothesis H0, since pvalue, 0.0301 is less than significance level, 0.05, and find evidence that the proprtion is greater than 40%.