Question

ABC Company prints text books. They use two modes of transportation to ship, rail and truck. In the 20 years during which they have operated, only 2 percent of the packages carried by rail and only 3.5 percent of the packages carried by truck have been lost. The claims manager receives a call and is informed that a package containing text books sent by ABC Company has been lost. ABC sends 60% of the packages by rail and 40% by truck. The text books are indeed lost. What is the probability the text books were shipped by truck

Answer 1

53.85% probability the text books were shipped by truck

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

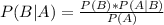
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Textbooks lost.

Event B: Shipped by truck.

40% of the packages sent by truck.

This means that
`P(B) = 0.4`

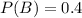
3.5 percent of the packages carried by truck have been lost.

This means that
`P(A|B) = 0.035`

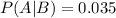
Probability package is lost:

60% probability it is sent by rail. Of those, 2% are lost.

40% sent by truck. Of those, 3.5% are lost.

So

`P(A) = 0.6*0.02 + 0.4*0.035 = 0.026`

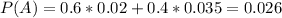
What is the probability the text books were shipped by truck

`P(B|A) = (P(B)*P(A|B))/(P(A)) = (0.4*0.035)/(0.026) = 0.5385`

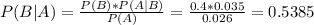
53.85% probability the text books were shipped by truck