Question

Two wires are hanging horizontally and parallel to one another and they are spaces 5.4 cm apart. The bottom wire carries a current of 2.3 Amps to the right and has a mass per unit length μ = 2.6 × 10 − 4 k g m. How much current must flow through the upper wire and in which direction (right or left) does the current flow in order to have the bottom wire hover (have the magnetic force balance the gravitational force mg)?

Answer 1

299.11 A

Step-by-step explanation:

You first equal the magnetic force on the upper wire with the gravitational force:

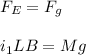`F_E=F_g\\\\i_1LB=Mg` ( 1 ) (first term is the magnetic force produced by the magnetic force of the second wire)

i1: current of the upper wire

L: length

M: mass of the upper wire

B: magnetic field generated by the second wire

Next, you calculate the magnetic field produced by the other wire:

`B=(\mu_o i_2)/(2\pi r)` (2)

i2: current of the second wire

r: distance between wires

mo: magnetic permeability of vacuum = 4pi*10^-7 T/A

Next, you replace the expression (2) into the expression (1) in order to obtain an expression for i2:

`i_1L((\mu_oi_2)/(2\pi r))=Mg\\\\i_2=(M)/(L)(2\pi r g)/(\mu_oi_1)`

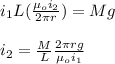
M/L = is the mass per unit length of the first wire

Finally, you replace the values of the parameters:

`i_2=(2.6*10^(-4)kg/m)(2\pi (0.054m)(9.8m/s^2))/((4\pi*10^(-7)T/A)(2.3A))\\\\i_2=299.11A`

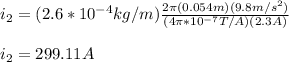
hence, the current in the second wire must be 299.11A