Question

Quality Motors has three plants. Plant 1 produces​ 35% of the car​ output, plant 2 produces​ 20% and plant 3 produces the remaining​ 45%. One percent of the output of plant 1 is​ defective, 1.8% of the output of plant 2 is defective and​ 2% of the output of plant 3 is defective. The annual total production of Quality Motors is​ 1,000,000 cars. A car is chosen at random from the annual output and is found defection. Use​ Bayes' Rule to find the probability that it came from plant 2.

Answer 1

The probability that it came from plant 2 is 0.224.

Explanation:

We are given that Quality Motors has three plants. Plant 1 produces​ 35% of the car​ output, plant 2 produces​ 20% and plant 3 produces the remaining​ 45%.

One percent of the output of plant 1 is​ defective, 1.8% of the output of plant 2 is defective and​ 2% of the output of plant 3 is defective.

Let the Probability that car output is produced by Plant 1 = P(A) = 0.35

Probability that car output is produced by Plant 2 = P(A) = 0.20

Probability that car output is produced by Plant 3 = P(A) = 0.45

Also, let D = event that output is defective

So, Probability that output defective given that it was produced by plant 1 = P(D/A) = 0.01

Probability that output defective given that it was produced by plant 2 = P(D/B) = 0.018

Probability that output defective given that it was produced by plant 3 = P(D/C) = 0.02

Now, a car is chosen at random from the annual output and is found defection so, the probability that it came from plant 2 is = P(B/D)

We will use the concept of Bayes' Theorem here to calculate the above probability.

SO, P(B/D) =
`(P(B) * P(D/B))/(P(A) * P(D/A) + P(B) * P(D/B)+P(C) * P(D/C))`

=
`(0.20 * 0.018)/(0.35 * 0.01 + 0.20 * 0.018+0.45 * 0.02)`

=
`(0.0036)/(0.0161)`

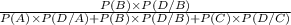
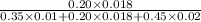
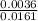
= 0.224

Hence, the required probability is 0.224.