Question

Bond X is a premium bond making semiannual payments. The bond pays a coupon rate of 12 percent, has a YTM of 10 percent, and has 16 years to maturity. Bond Y is a discount bond making semiannual payments. This bond pays a coupon rate of 10 percent, has a YTM of 12 percent, and also has 16 years to maturity. The bonds have a $1,000 par value. What is the price of each bond today?

Answer 1

Price of x bond = $1158.02

Price of y bond = $1000

Step-by-step explanation:

given data

bonds value = $1,000 par value

x bond

coupon rate = 12 percent = 0.12

YTM = 10 percent = 0.10 = 0.05 semi annual

maturity = 16 years = 32 semi annual

y bond

coupon rate = 10 percent = 0.10

YTM = 12 percent = 0.12 = 0.06 semi annual

maturity = 16 years = 32 semi annual

solution

For x bond

first we get here semi annual coupon payment that is express as

semi annual payment = bonds value × coupon rate × time period .........1

semi annual payment = $1000 × 0.12 × 0.5

semi annual payment = $60

and

Price of bond will be

Price of bond = semi annual payment ×
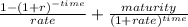`(1-(1+r)^(-time) )/(rate) + (maturity)/((1+rate)^(time))` ..........................2

put here value and we get

Price of bond = 60 ×
`(1-(1+0.05)^(-32) )/(0.05) + (1000)/((1+0.05)^(32))`

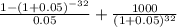
Price of bond = $1158.02

and

For y bond

semi annual payment = bonds value × coupon rate × time period .........3

semi annual payment = $1000 × 0.10 × 0.5

semi annual payment = $50

and

Price of bond will be

Price of bond = semi annual payment ×
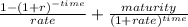`(1-(1+r)^(-time) )/(rate) + (maturity)/((1+rate)^(time))` ..........................4

put here value and we get

Price of bond = 50 ×
`(1-(1+0.06)^(-32) )/(0.06) + (1000)/((1+0.06)^(32))`

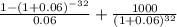
Price of bond = $1000