Question

laws of Sines with find the angle. Find each measurement indicated. Round your answers to the nearest tenth. Part 4​

Answer 1

10. Not enough information

11. B ≈ 12.0°

12. A ≈ 34.1°

Explanation:

10. Not enough information

11.

We need to use the Law of Sines, which states that for a triangle with lengths a, b, and c and angles A, B, and C:

`(a)/(sinA) =(b)/(sinB) =(c)/(sinC)`

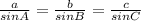
Here, we can say that AB = c = 38, C = 128, and AC = b = 10. Plug these in to find B:

`(b)/(sinB) =(c)/(sinC)`

`(10)/(sinB) =(38)/(sin128)`

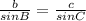
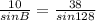
Solve for B:

B ≈ 12.0°

12.

Use the Law of Sines as above.

`(a)/(sinA) =(b)/(sinB)`

`(23)/(sinA) =(28)/(sin(43))`

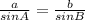
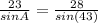
Solve for A:

A ≈ 34.1°