Question

What would be the maximum Y value on the circle whose equation is shown below. x^2+10x+y^2-4y=71

Answer 1

12.

Explanation:

The given equation is

`x^2+10x+y^2-4y=71`

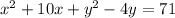
It can be written as

`(x^2+10x)+(y^2-4y)=71`

`(x^2+10x+5^2)+(y^2-4y+2^2)=71+5^2+2^2`

`(x+5)^2+(y-2)^2=71+25+4`

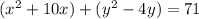
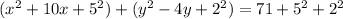
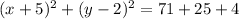
`(x+5)^2+(y-2)^2=10^2` ...(i)

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2` ...(ii)

where, (h,k) is center and r is radius.

From (i) and (ii), we get

`h=-5,k=2,r=10`

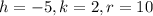
The center of circle is (-5,2) and radius is 10. So, the maximum value of y is

`Max(y)=k+r=2+10=12`

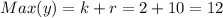
Therefore, the maximum value of y is 12.