Question

Users independently sign up for two online social networking sites, Lookbook and Quickgram. On average, 7.5 users sign up for Lookbook each minute, while on average 5.5 users sign up for Quickgram each minute. The number of users signing up for Lookbook and for Quickgram each minute are independent. A new user is defined as a new account, i.e., the same person signing up for both social networking sites will count as two new users. a. What is the probability that more than 10 new users will sign up for the Lookbook social networking site in the next minute

Answer 1

13.57% probability that more than 10 new users will sign up for the Lookbook social networking site in the next minute

Explanation:

To solve this question, we need to understand the poisson and the normal probability distribution.

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\lambda)*\lambda^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\lambda` is the mean in the given interval. The variance is the same as the mean.

Normal probability distribution:

Problems of normally distributed samples are solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

To approximate the Poisson distribution, we use
`\mu = \lambda, \sigma = √(\lambda)`

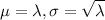
On average, 7.5 users sign up for Lookbook each minute

This means that
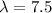`\lambda = 7.5`. So

`\mu = 7.5, \sigma = √(7.5) = 2.7386`

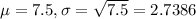
What is the probability that more than 10 new users will sign up for the Lookbook social networking site in the next minute

Using continuity correction, this is P(X > 10 + 0.5) = P(X > 10.5), which is 1 subtracted by the pvalue of Z when X = 10.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (10.5 - 7.5)/(2.7386)`

`Z = 1.1`

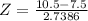
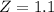
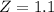`Z = 1.1` has a pvalue of 0.8643.

1 - 0.8643 = 0.1357

13.57% probability that more than 10 new users will sign up for the Lookbook social networking site in the next minute