Question

laws of Sines with find the angle. Find each measurement indicated. Round your answers to the nearest tenth. Show your work please. Part 2​

Answer 1

4. Z ≈ 46.1°

5. T ≈ 45.2°

6. F ≈ 15.0°

Explanation:

4.

We need to use the Law of Sines, which states that for a triangle with legnths a, b, and c and angles A, B, and C:

`(a)/(sinA) =(b)/(sinB) =(c)/(sinC)`

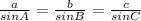
Here, we can say that ZY = a = 30, X = A = 110, XY = b = 23, and Z = B. Plug these in to find Z:

`(a)/(sinA) =(b)/(sinB)`

`(30)/(sin(110)) =(23)/(sinZ)`

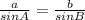
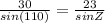
Solve for Z:

Z ≈ 46.1°

5.

Use the Law of Sines as above.

`(a)/(sinA) =(b)/(sinB)`

`(26)/(sin(76)) =(19)/(sinT)`

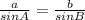
Solve for T:

T ≈ 45.2°

6.

Again, use the Law of Sines as before.

`(a)/(sinA) =(b)/(sinB)`

`(29)/(sin(137)) =(11)/(sinF)`

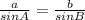
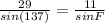
Solve for F:

F ≈ 15.0°