Answer: Initial population = 500
Decay factor of population =0.80
Explanation:
We know that , the general exponential function is given by :-
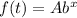 ...(i)
...(i)
Where , A = initial value
b= growth factor ( if b>1)
or b= decay factor ( if b<1)
x= Time perid
Given : A population of bacteria in a lab, p(t), can be modeled by the function
 , where t represents the number of days since the population was first counted.
, where t represents the number of days since the population was first counted.
By comparing
 to (i) , we get
to (i) , we get
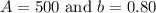
i..e Initial population = 500
Also as 0.80<1 , therefore we have decay factor of population =0.80