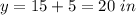Question

The length of a rectangle is 5 inches more than its width,x.The area of a rectangle can be represented by the equation x^2=+5X=300.What are the meausres of the width and the length?

Answer 1

Width = 15 inches

length = 20 inches

Explanation:

Let

width = x

According to the question the length of the rectangle is 5 inches more than it width. Therefore,

length = x + 5

Area of a rectangle = LW

where

L = length

W = width

Area of the rectangle

x² + 5x = 300

x² + 5x - 300 = 0

Find the number you can multiply to give you -300 and add to give you 5. The numbers are -15 and 20

x² - 15x + 20x -300 = 0

x(x - 15) + 20(x - 15)

(x - 15)(x + 20) = 0

x = 15 or - 20

we can't use - 20 since it is negative.

Recall

width = x = 15

length = x + 5 = 15 + 5 = 20

Width = 15 inches

length = 20 inches

Answer 2

`Width=15\ inLength=20\ in`

Explanation:

x^2=+5X=300

Let

x = the width of the rectangle

y = the length of the rectangle

we know that

the area of the rectangle is equal to

A=xy ___ equation 1

y=x+5 ___equation 2

substitute equation 2 in equation 1

`A=x(x+5)A=x^(2)+5x`

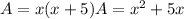
`x^(2) +5x=300` ------> given problem

so

the area of the rectangle is equal to

`A=300\ in^(2)`

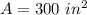
Solve the quadratic equation

`x^(2) +5x-300=0`

we know that

The formula to solve a quadratic equation of the form
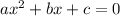`ax^(2) +bx+c=0` is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

we have

`x^(2) +5x-300=0`

so

`a=1\\b=5\\c=-300`

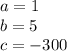
substitute in the formula

`x=\frac{-5 \pm\sqrt{5^(2)-4(1)(-300)}} {2(1)}`

`x=\frac{-5 \pm √(1225)} {2}`

`x=\frac{-5 \pm 35} {2}`

`x=\frac{-5+35} {2}=15`

`x=\frac{-5-35} {2}=-20`

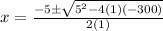
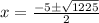
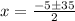
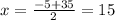
The solution is

`x=15\ in`

Find the value of y

y=x+5

`y=15+5=20\ in`

`Width=15\ inLength=20\ in`