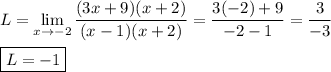Question

Find all the real numbers a, so that the following limit exists.

L=
`\lim_(x \to \ -2) (3x^(2) +ax+a+3)/(x^(2)+x-2 )`


Calculate the value of L and a

Answer 1

• a = 15
• L = -1

Explanation:

In order for the limit to exist at x=-2, the denominator factor of (x+2) must be canceled by a numerator factor of (x+2). Synthetic division (see below) shows the remainder when the numerator is divided by (x+2) is (15-a). In order for that remainder to be zero, so that (x+2) is a factor, we must have ...

`15-a=0\\\\\boxed{a=15}`

__

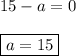
The same synthetic division shows the other numerator factor to be ...

(3x +(a -6))

For a=15, this is ...

(3x +9)

and the expression becomes ...

`L= \lim\limits_(x \to -2) ((3x+9)(x+2))/((x-1)(x+2))=(3(-2)+9)/(-2-1)=(3)/(-3)\\\\\boxed{L=-1}`