Answer:
The probability that, in the coming year, Company B’s total claim amount will exceed Company A’s total claim amount is 0.4013.
Explanation:
Let,
A = the total claim amount made for Company A during the coming year
B = the total claim amount made for Company B during the coming year
The random variable A follows a Normal distribution with parameters,
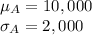
The random variable B follows a Normal distribution with parameters,
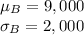
Compute the probability that in the coming year, Company B’s total claim amount will exceed Company A’s total claim amount as follows:
The variable is then: A - B < 0.
Compute the mean and standard deviation of A - B as follows:

Compute the probability of A - B < 0 as follows:
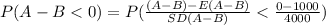
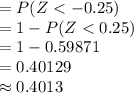
Thus, the probability that, in the coming year, Company B’s total claim amount will exceed Company A’s total claim amount is 0.4013.