Question

The manufacturer of an airport baggage scanning machine claims it can handle an average of 553 bags per hour. (a-1) At α = .05 in a left-tailed test, would a sample of 16 randomly chosen hours with a mean of 533 and a standard deviation of 47 indicate that the manufacturer’s claim is overstated? Choose the appropriate hypothesis. H1: μ < 553. Reject H1 if tcalc > –1.753 H0: μ < 553. Reject H0 if tcalc > –1.753 H1: μ ≥ 553. Reject H1 if tcalc < –1.753 H0: μ ≥ 553. Reject H0 if tcalc < –1.753 b a d c (a-2) State the conclusion. tcalc = –1.702. There is not enough evidence to reject the manufacturer’s claim. tcalc = –1.702. There is significant evidence to reject the manufacturer’s claim. b a

Answer 1

H1 : μ < 553. Reject H1 if tcalc > –1.753.

There is not enough evidence to reject the manufacturer’s claim.

Explanation:

We are given that the manufacturer of an airport baggage scanning machine claims it can handle an average of 553 bags per hour.

A sample of 16 randomly chosen hours with a mean of 533 and a standard deviation of 47 is given.

Let
`\mu` = average bags that an airport baggage scanning machine can handle.

SO, Null Hypothesis,
`H_0` :
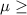`\mu \geq` 553 bags {means that the manufacturer’s claim is not overstated}

Alternate Hypothesis,
`H_0` :
`\mu` < 553 bags {means that the manufacturer’s claim is overstated}

The test statistics that would be used here One-sample t-test statistics as we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean = 533 bags

s = sample standard deviation = 47

n = sample of hours = 16

So, the test statistics =
`(533-553)/((47)/(√(16) ) )` ~
`t_1_5`

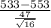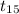
= -1.702

The value of t test statistics is -1.702.

Now, at 0.05 significance level the t table gives critical value of -1.753 at 15 degree of freedom for left-tailed test.

Since our test statistic is more than the critical value of t as -1.702 > -1.753, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that the manufacturer’s claim is not overstated and an airport baggage scanning machine can handle an average of 553 bags per hour.