Question

Eric's class consists of 12 males and 16 females. If 3 students are selected at random, find the probability that they

are all male

Answer 1

C. 55/819

Explanation:

got it right on edge

Answer 2

The probability that all are male of choosing '3' students

P(E) = 0.067 = 6.71%

Explanation:

Let 'M' be the event of selecting males n(M) = 12

Number of ways of choosing 3 students From all males and females

`n(M) = 28C_(3) = (28!)/((28-3)!3!) =(28 X 27 X 26)/(3 X 2 X 1 ) = 3,276`

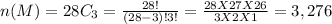
Number of ways of choosing 3 students From all males

`n(M) = 12C_(3) = (12!)/((12-3)!3!) =(12 X 11 X 10)/(3 X 2 X 1 ) =220`

The probability that all are male of choosing '3' students

`P(E) = (n(M))/(n(S)) = (12 C_(3) )/(28 C_(3) )`

`P(E) = (12 C_(3) )/(28 C_(3) ) = (220)/(3276)`

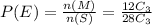
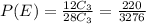
P(E) = 0.067 = 6.71%

Final answer:-

The probability that all are male of choosing '3' students

P(E) = 0.067 = 6.71%