Answer:
a) t = 5.40 s
b)
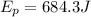
c)
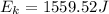
d) mv = 74.6 kgm/s
Step-by-step explanation:
We have:
v₀ : initial speed = 45.6 m/s
θ: 30 °
h: height = 20 m
m: projectile's mass = 1.5 kg
a) The flight time of the projectile as it lands at Q (when it impacts on the ground in the parabolic motion) can be calculated using the following equation:
 (1)
(1)
Where g is the gravity = 9.81 g/s²
By solving equation (1) for t, we have:

b) The gravitational potential energy (
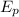 ) of the projectile at point P (at the maximum height in the parabolic motion) is the following:
) of the projectile at point P (at the maximum height in the parabolic motion) is the following:
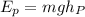
Where
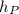 : is the height at the point P. This can be calculated using the following equation:
: is the height at the point P. This can be calculated using the following equation:
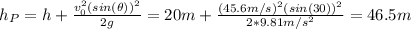
Now, the gravitational potential energy is:
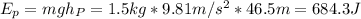
c) The kinetic energy of the projectile at point R (the same height as the edge of the building in the parabolic motion) is:
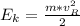
Where
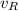 is the velocity at the point R, which is:
is the velocity at the point R, which is:
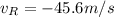
Now, the kinetic energy is:
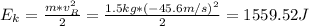
d) The magnitude and direction of impulse the projectile impacts on the ground can be calculated using the equation:
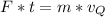
Where F: is the force
The velocity at the point Q is:
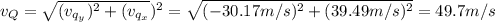
Hence, the magnitude and direction of impulse is:

I hope it helps you!