Answer:
b) on the circle
The point lies on the circle S =0
Explanation:
Step(i):-
Given center of the circle = H(4,0)
Radius of the circle 'r' = 10
Equation of the circle
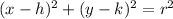
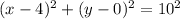
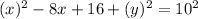
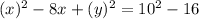
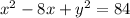
Step(ii):-
S =0 is a circle and P(x₁ , y₁) be a point in its plane
Then (i) P lies inside the circle S = 0 ⇔ S₁₁ < 0
ii) P lies outside the circle S = 0 ⇔ S₁₁ > 0
iii) P lies on the circle S = 0 ⇔ S₁₁ = 0
now
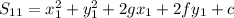
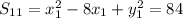
Given point ( -2 , 8)
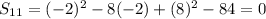
P lies on the circle S = 0 ⇔ S₁₁ = 0