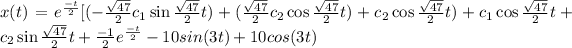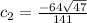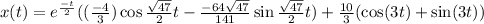Question

mass weighing 16 pounds stretches a spring 8 3 feet. The mass is initially released from rest from a point 2 feet below the equilibrium position, and the subsequent motion takes place in a medium that offers a damping force that is numerically equal to 1 2 the instantaneous velocity. Find the equation of motion x(t) if the mass is driven by an external force equal to f(t)

Answer 1

The answer is

"
`x(t)= e^(-t)/(2)(((-4)/(3))\cos(√(47))/(2)t- (-64√(47))/(141) \sin(√(47))/(2)t)+(10)/(3)(\cos(3t)+ \sin (3t))`".

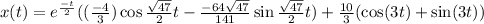Step-by-step explanation:

Taking into consideration a volume weight = 16 pounds originally extends a springs
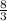`(8)/(3)` feet but is extracted to resting at 2 feet beneath balance position.

The mass value is =

`W=mg\\m=(w)/(g)\\m=(16)/(32)\\m= (1)/(2) slug\\`

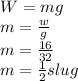
The source of the hooks law is stable,

`16= (8)/(3) k \\\\8k=16 * 3 \\\\k=16* (3)/(8) \\\\k=6 (lb)/(ft)\\\\`

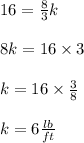
Number
`(1)/(2)` times the immediate speed, i.e .. Damping force

`(1)/(2) (d^2 x)/(dt^2) = -6x-(1)/(2)(dx)/(dt)+10 \cos 3t \\\\(1)/(2) (d^2 x)/(dt^2)+ (1)/(2)(dx)/(dt)+6x =10 \cos 3t \\ \\(d^2 x)/(dt^2) +(dx)/(dt)+12x=20\cos 3t \\\\`

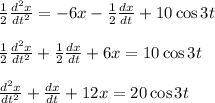
The m^2+m+12=0 and m is an auxiliary equation,

`m=(-1 \pm √(1-4(12)))/(2)\\\\m=(-1 \pm √(47i))/(2)\\\\\ m1= (-1 + √(47i))/(2) \ \ \ \ or\ \ \ \ \ m2 =(-1 - √(47i))/(2)`

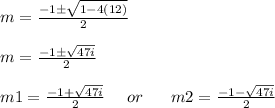
Therefore, additional feature

`x_c (t) = e^{(-t)/(2)}[C_1 \cos (√(47))/(2)t+ C_2 \sin (√(47))/(2)t]`

Use the form of uncertain coefficients to find a particular solution.

Assume that solution equation,

`x_p = Acos(3t)+B sin(3t) \\x_p'= -3A sin (3t) + 3B cos (3t)\\x_p}^{n= -9 Acos(3t) -9B sin (3t)\\`

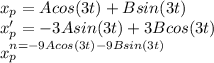
These values are replaced by equation ( 1):

`(d^2x)/(dt)+(dx)/(dt)+ 12x=20 \cos(3t) -9 Acos(3t) -9B sin (3t) -3Asin(3t)+3B cos (3t) + 12A cos (3t) + 12B sin (3t)\\\\3Acos 3t + 3B sin 3t - 3Asin 3t + 3B cos 3t= 20cos(3t)\\(3A+3B)cos3t -(3A-3B)sin3t = 20 cos (3t)\\`

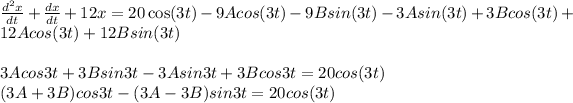
Going to compare cos3 t and sin 3 t coefficients from both sides,

The cost3 t is 3A + 3B= 20 coefficients

The sin 3 t is 3B -3A = 0 coefficient

The two equations solved:

`3A+3B = 20 \\\frac{3B -3A=0}{}\\6B=20\\B= (20)/(6)\\B=(10)/(3)\\`

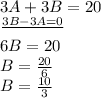
Replace the very first equation with the meaning,

`3B -3A=O\\3((10)/(3))-3A =0\\A= (10)/(3)\\`

equation is

`x_p\\\\(10)/(3) cos (3 t) + (10)/(3) sin (3t)`

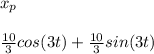
The ultimate plan for both the equation is therefore

`x(t)= e^(-t)/(2) (c_1 cos (√(47))/(2)t)+c_2\sin(√(47))/(2)t)+(10)/(3)\cos (3t)+(10)/(3)\sin (3t)`

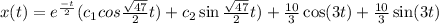
Initially, the volume of rest x(0)=2 and x'(0) is extracted by rest i.e.

Throughout the general solution, replace initial state x(0) = 2,

Replace x'(0)=0 with a general solution in the initial condition,

`x(t)= e^(-t)/(2) [(c_1 cos (√(47))/(2)t)+c_2\sin(√(47))/(2)t)+(10)/(3)\cos (3t)+(10)/(3)\sin (3t)]\\\\`

`x(t)= e^(-t)/(2) [(-(√(47))/(2)c_1\sin(√(47))/(2)t)+ ((√(47))/(2)c_2\cos(√(47))/(2)t)+c_2\cos(√(47))/(2)t) +c_1\cos(√(47))/(2)t +c_2\sin(√(47))/(2)t + (-1)/(2)e^{(-t)/(2)} -10 sin(3t)+10 cos(3t) \\\\`

`c_2=(-64√(47))/(141)`

`x(t)= e^(-t)/(2)(((-4)/(3))\cos(√(47))/(2)t- (-64√(47))/(141) \sin(√(47))/(2)t)+(10)/(3)(\cos(3t)+ \sin (3t))`