Question

At a certain university, 22% of students fail general chemistry on their first attempt. Professor Brown teaches at this university and believes that the rate of first-time failure in his general chemistry classes is 45%. He samples 86 students from last semester who were first-time enrollees in general chemistry and finds that 19 of them failed his course. Using α = 0.05, can you conclude that the percentage of failures differs from 45%?

Answer 1

We conclude that the percentage of failures differs from 45%.

Explanation:

We are given that Professor Brown teaches at this university and believes that the rate of first-time failure in his general chemistry classes is 45%.

He samples 86 students from last semester who were first-time enrolls in general chemistry and finds that 19 of them failed his course.

Let p = percentage of failures in general chemistry course.

SO, Null Hypothesis,
`H_0` : p = 45% {means that the percentage of failures equals 45%}

Alternate Hypothesis,
`H_A` : p
`\\eq` 45% {means that the percentage of failures differs from 45%}

The test statistics that would be used here One-sample z test for proportions;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of first-time enrolls in general chemistry who failed in this course =
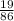`(19)/(86)` = 0.22

n = sample of students = 86

So, the test statistics =
`\frac{0.22-0.45}{\sqrt{(0.22(1-0.22))/(86) } }`

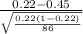
= -5.149

The value of z test statistics is -5.149.

Now, at 0.05 significance level the z table gives critical values of -1.96 and 1.96 for two-tailed test.

Since our test statistic doesn't lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the percentage of failures differs from 45%.