Answer:
a. acceleration (a) = 4.9 m/s²
b.
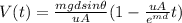
c. see the attached diagram below
d V = 0.048 m/s
e. The viscosity u = 0.27 Ns/m²
Step-by-step explanation:
Given that :
m = 5 kg
A = ( 0.1 m )²
d = 0.20 mm
θ = 30 °
By applying Newton's second Law ; we have
F = mgsinθ -
 (since no friction ; then
(since no friction ; then
ma = mg sinθ
a = gsin θ
a = 9.8 × sin 30
a = 4.9 m/s²
b) By applying Newton's second law at any instant .
ma = mgsin θ -

and
 = T×A =
= T×A =
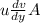 -
-
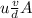
Also; ma =
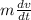
∴ ma = mg sin θ -
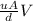
separating the variables ; we have
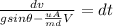
By integrating using limits ; we have:

∴
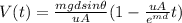
c) The curve for V(t) plot is attached in the diagram below.
d)
To find the speed after 1 sec; we have:
at t = 1.0 sec;
V =
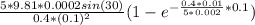
V = 0.048 m/s
e) In order to determine the viscosity for which V(0.1) = 0.3 m/s ; we have the following.
∴
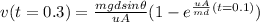

The viscosity u = 0.27 Ns/m²