Answer:
2cis(20°)
Explanation:
we are given that
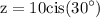
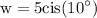
We want to find z/w . To do so, divide 10cis(30°) by w = 5cis(10°) which yields:
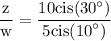
recall that,
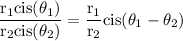
consider,
Therefore, utilizing the formula yields:
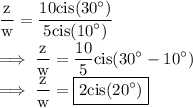
and we're done!
NB: cis(x) is also known as cos(x)+i×sin(x)