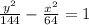Question

In a hyperbola, the horizontal distance from the center to the vertices is a=8, the vertical distance from the center to the vertices is b=12, the hyperbola opens up and down, and the center is (0,0). Find the equation of the hyperbola.

Answer 1

The equation of the parabola is given as follows;

`(y ^2)/(144) - (x ^2)/(64) = 1`

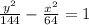
Explanation:

Here we have the general equation of a vertical hyperbola, where the y term is positive is given by the relation;

`((y - k )^2)/(b^2) - ((x - h )^2)/(a^2) = 1`

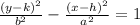
Where:

(h, k) are the coordinates of the center which is given as (0, 0)

a = Horizontal distance from the center of the hyperbola = 8

b = Vertical distance from the center of the hyperbola = 12

Plugging in the values, we have the equation of the parabola given as follows;

`((y - 0 )^2)/(12^2) - ((x - 0 )^2)/(8^2) = 1 = (y ^2)/(12^2) - (x ^2)/(8^2) = 1`

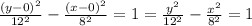
Hence the equation of the parabola is given as follows;

`(y ^2)/(144) - (x ^2)/(64) = 1`