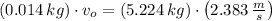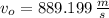Question

A 14.3-g bullet is fired into a 5.21 kg block of wood. The block is attached to a spring that has a spring force constant of 450 N/m. The block and bullet continue to move, compressing the spring by 22.0 cm before the whole system momentarily comes to a stop. The coefficient of kinetic friction between block and the surface on which the block is resting is 0.35. Determine the initial speed of bullet.

Answer 1

The initial speed of the bullet is
`v_(o) = 889.199\,(m)/(s)`.

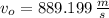Step-by-step explanation:

The collision between bullet and block is inelastic and let suppose that motion occurs on a horizontal surface, so that changes in gravitational potential energy can be neglected. Initially, the intial speed of the bullet-block system can be determined with the help of the Work-Energy Theorem and the Principle of Energy Conservation:

`K = U_(k) + W_(loss)`

`(1)/(2)\cdot (5.224\,kg)\cdot v^(2) = (1)/(2)\cdot \left(450\,(N)/(m)\right)\cdot (0.22\,m)^(2) + (0.35)\cdot (5.224\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right) \cdot (0.22\,m)`

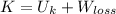
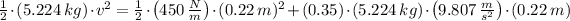
The initial speed of the bullet-block system is:

`v \approx 2.383\,(m)/(s)`

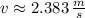
Now, the initial speed of the bullet is determined by applying the Principle of Momentum Conservation:

`(0.014\,kg)\cdot v_(o) = (5.224\,kg)\cdot \left(2.383\,(m)/(s) \right)`

`v_(o) = 889.199\,(m)/(s)`