Answer:
7.5 Units
Explanation:
Angle ABC of triangle ABC is a Right angle. The sides of ABC are the diameters of semicircles
The area of the semicircle on AB equals 8pi
Area of a semicircle
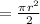
Therefore:

Next, the arc of the semicircle on AC has length 8.5pi.
Length of arc of a semicircle =
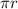
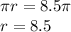
Using Pythagoras theorem
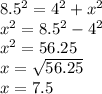
Radius of the semicircle of BC=7.5 Units