Answer:
The amount of C remaining after time t is
![N_C__(R)} =N_D = (N_0 -N_0 e^(\lambda_A t)) - (N_0 -N_0 e^(-\lambda_A t))e^(-\lambda_B ) [e^(-\lambda_C ) ]](https://img.qammunity.org/2021/formulas/physics/middle-school/qq6qwwmqbit4eow6lbr992x861ugsfeue5.png)
Step-by-step explanation:
We can represent the decay sequence as
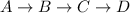
The reason we added D is because we are told from the question that C is also radioactive so it has the tendency to decay
Generally for every decay the remaining radioactive element can be obtained as
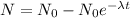
Where N is the amount of the remaining radioactive material
 is the original amount amount of the radioactive material before decay
is the original amount amount of the radioactive material before decay
and
 is the decay constant
is the decay constant
Now for the decay from
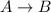 amount of radioactive element B formed from A after time t can be obtained as
amount of radioactive element B formed from A after time t can be obtained as
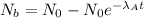
Where
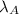 is the decay constant of A
is the decay constant of A
Now for the decay from
 amount of radioactive element C formed from A after time t can be obtained as
amount of radioactive element C formed from A after time t can be obtained as
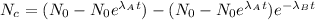
Where
 is the decay constant of B
is the decay constant of B
Now for the decay from
 amount of radioactive element D formed from A after time t can be obtained as
amount of radioactive element D formed from A after time t can be obtained as
![N_C__(R)} =N_D = (N_0 -N_0 e^(\lambda_A t)) - (N_0 -N_0 e^(-\lambda_A t))e^(-\lambda_B ) [e^(-\lambda_C ) ]](https://img.qammunity.org/2021/formulas/physics/middle-school/qq6qwwmqbit4eow6lbr992x861ugsfeue5.png)
So this amount of D is the reaming amount of the radioactive material C