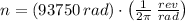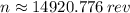Question

A 3.45-kg centrifuge takes 100 s to spin up from rest to its final angular speed with constant angular acceleration. A point located 8.00 cm from the axis of rotation of the centrifuge moves with a speed of 150 m/s when the centrifuge is at full speed. (a) What is the angular acceleration (in rad/s2) of the centrifuge as it spins up? (b) How many revolutions does the centrifuge make as it goes from rest to its final angular speed?

Answer 1

a)
`\alpha = 18.75\,(rad)/(s^(2))`, b)
`n \approx 14920.776\,rev`

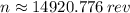
Step-by-step explanation:

a) The final angular speed is:

`\omega = (v)/(R)`

`\omega = (150\,(m)/(s) )/(0.08\,m)`

`\omega = 1875\,(rad)/(s)`

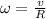
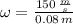
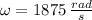
The angular acceleration experimented by the centrifuge is determined by means of the following kinematic expression:

`\alpha = (\omega - \omega_(o))/(\Delta t)`

`\alpha = (1875\,(rad)/(s) - 0\,(rad)/(s) )/(100\,s)`

`\alpha = 18.75\,(rad)/(s^(2))`

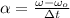
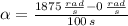
b) The change in angular position is:

`\Delta \theta = (\omega^(2)-\omega_(o)^(2))/(2\cdot \alpha)`

`\Delta \theta = (\left(1875\,(rad)/(s) \right)^(2)-\left(0\,(rad)/(s) \right)^(2))/(2\cdot \left(18.75\,(rad)/(s^(2)) \right))`

`\Delta \theta = 93750\,rad`

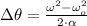
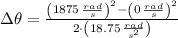
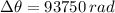
Lastly, the total amount of revolutions made by the centrifuge is:

`n = (93750\,rad)\cdot \left((1)/(2\pi)\,(rev)/(rad) \right)`

`n \approx 14920.776\,rev`