Question

What is a common factor for the two fractional terms StartFraction 5 over 8 EndFraction x andStartFraction 11 over 8 EndFraction x y? The terms can be written as 5StartFraction 1 over 8 EndFraction(x) and 11StartFraction 1 over 8 EndFractionxy. 5 StartFraction 1 over 8 EndFraction x StartFraction 5 over 8 EndFraction y

Answer 1

B. 1/8x

Explanation:

Answer 2

`(1)/(8x)`

Explanation:

Given two fractional terms
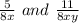`(5)/(8x)\ and\ (11)/(8xy)`. Their common factor is a value or function that can go in both fractional terms. The terms can be written as shown.

`(5)/(8x) = 5 *(1)/(8x)`

`(11)/(8xy) = 11 * (1)/(8x) * (1)/(y)`

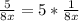
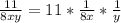
It can be seen from the both equations that they both have
`(1)/(8x)` as one of their factors i.e 1/8x is common to both fractional terms. This gives the common factor for the two fractional terms as
`(1)/(8x)`