Question

Can somebody please help me with this

Answer 1

∠PYG = 137°

Explanation:

We know that a straight line is equal to 180°, so by looking at the image we can tell that if we added both of these angles together they would be equal to the straight line.

We can make an equation by adding these two angles together and setting them equal to 180.

`2p+153+6p+91=180`

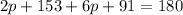
We can combine like terms.

`8p+244=180`

Subtract 244 from both sides.

`8p=-64`

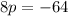
Divide.

p = -8

Now that we have found what p is equal to, we can plug it in to find the measure of ∠PYG.

`2*-8+153`

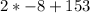
= 137

~

If you wanted to double check this answer, we can plug in -8 for p on the other side and make sure both would be equal to 180.

Like this...

`6*-8+91`

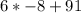
= 43

And we know that...

137 + 43 = 180

~

So...

∠PYG = 137°

∠HYG = 43°