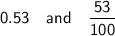Question

Se the number line to answer the question.

A number line has end points marked at 5 tenths and 6 tenths with 9 tick marks between. Point A is labeled on the third mark after 5 tenths.


Select all of the following that give the value of point A.


A.

53

100

B.

5

3

100

C.

53

10

D.

0.53


E.

5.3

Answer 1

Answer: i need points

Explanation:

Answer 2

`\sf 0.53\quad and \quad (53)/(100)`

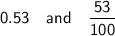
Explanation:

Convert the end points to decimals:

`\textsf{5 tenths}=(5)/(10)=5 / 10=0.5`

`\textsf{6 tenths}=(6)/(10)=6/ 10=0.6`

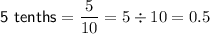
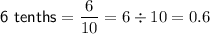
If the number line has 9 tick marks between the endpoints, there will be 10 equal spaces (see attachment), so the tick marks denote hundredths.

The difference between 0.6 and 0.5 = 0.1

Divide this by 10: 0.1 ÷ 10 = 0.01

Therefore, each tick mark on the number line denotes hundredths and is 0.01 greater than the previous tick mark.

If Point A is labeled on the third mark after 5 tenths then:

A = 0.5 + 0.01 + 0.01 + 0.01 = 0.53

0.53 as a fraction:

`\implies 0.53 = (0.53)/(1)=(0.53 * 100)/(1 * 100)=(53)/(100)`

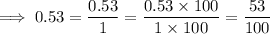
Therefore, point A is:

`\sf 0.53\quad and \quad (53)/(100)`