We have been given that Bobby's investment of $225,000 loses value at a rate of 3% per year. We are asked to find the value of the investment after 10 years.
We will us exponential decay function to solve our given problem.
We know that an exponential function is in form
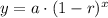 , where,
, where,
y = Final amount,
a = Initial amount,
r = Decay rate in decimal form,
x = Time.
Let us convert 3% into decimal.
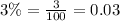
Upon substituting
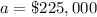 ,
,
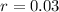 and
and
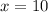 , we will get:
, we will get:
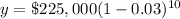
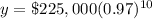
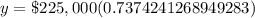
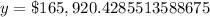
Upon rounding to nearest dollar, we will get;
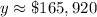
Therefore, the value of the investment after 10 years would be
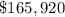 .
.