Correct question:
A food company sells salmon to various customers. The mean weight of the salmon is 44 lb with a standard deviation of 3 lbs. The company ships them to restaurants in boxes of 9 salmon, to grocery stores in cartons of 16 salmon, and to discount outlet stores in pallets of 64 salmon. To forecast costs, the shipping department needs to estimate the standard deviation of the mean weight of the salmon in each type of shipment. Complete parts (a) and (b) below.
a. Find the standard deviations of the mean weight of the salmon in each type of shipment.
b. The distribution of the salmon weights turns out to be skewed to the high end. Would the distribution of shipping weights be better characterized by a Normal model for the boxes or pallets?
Answer:
Given:
Mean, u = 44
Sd = 3
The company ships in boxes of 9, cartons of 16 and pallets of 64.
a) For the standard deviations of the mean weight of the salmon in each type of shipment, lets use the formula:
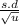
i) For the standard deviation of the mean weight of salmon in boxes of 9, we have:
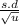
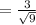
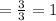
The standard deviation = 1
ii) For the standard deviation of the mean weight of salmon in cartons of 16, we have:
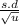
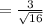
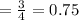
Standard deviation = 0.75
iii) For the standard deviation of the mean weight of salmon in pellets of 64, we have:
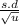
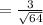
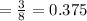
Standard deviation = 0.375
b) The distribution of shipping weights would be better characterized by a Normal model for the pallets, because regardless of the underlying distribution, the sampling distribution of the mean approaches the Normal model as the sample increases.