Question

In an arithmetic sequence, a17 = -40 and

a28 = -73. Explain how to use this information to write a recursive formula for this sequence.
please answer!

Answer 1

`a_n=-3n+11`

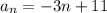
Explanation:

We are given the values of two terms in this arithmetic sequence:
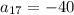`a_(17)=-40` and
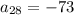`a_(28)=-73`. We want to find the recursive formula of this sequence, which will be in the form
`a_n=a_1+d(n-1)`, where
`a_1` is the first term and d is the common difference.

Here, we can pretend that
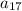`a_(17)` will replace the
`a_1` term, while
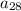`a_(28)` replaces the
`a_n` term. This way, n becomes 28 and 1 becomes 17. Now, we can write:

`a_n=a_1+d(n-1)`

`a_(28)=a_(17)+d(28-17)`

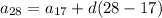
Substitute in the values we know:

`a_(28)=a_(17)+d(28-17)`

`-73=-40+d(28-17)`

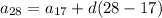
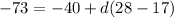
Solve for d:

`-73=-40+d(28-17)`

`-73=-40+d(11)`

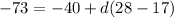
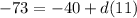
11d = -33

d = -3

Now, we need to find our first term. We can do this by replacing
`a_n` with
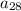`a_(28)` again, but this time, we're actually going to use
`a_1`:

`a_(28)=a_1+d(28-1)`

Plug in the values we know:

`a_(28)=a_1+d(28-1)`

`-73=a_1-3(27)`

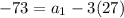
Solve for
`a_1`:

-73 =
`a_1` - 81

`a_1` = 8

Put these altogether:

`a_n=8-3(n-1)=-3n+11`

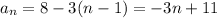
Thus, the recursive formula is
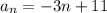`a_n=-3n+11`.

Answer 2

`a_(17)`= -40

a + 16d = -40 ...... -(i)

`a_(28)`= -73

a + 27d = -73 .......(ii)

Subtracting (i) and (ii)

a + 16 d - a - 27 d = - 40 + 73

-11d = 33

d = -3

a = -40 - 16d = -40 - 16(-3) = 8

`a_n` = 8 + (n-1)-3

= 8 -3n +3

= -3n + 11

Hence recursive formula :

`a_n`= -3n + 11