Question

The daily average temperature in Santiago, Chile, varies over time in a periodic way that can be modeled approximately by a trigonometric function.

Assume the length of the year (which is the period of change) is exactly 365days long. The hottest day of the year, on average, is January 777, when the average temperature is about 29 degrees C.

The average temperature at the coolest day of the year is about 14 degrees C.

Find the formula of the trigonometric function that models the daily average temperature T in Santiago t days into the year. (t = 1 on January 1) Define the function using radians.

What is the average temperature in Santiago on January 31? Round your answer, if necessary, to two decimal places.

Answer 1

7.5cos(2
`\pi`/365(t-7))+21.5

b) 28.37

Explanation:

Answer 2

a) the trigonometric function is;

`y = 7.5 sin ( (2 \pi)/(365)t + (337 \pi)/(730))+ 21.5`

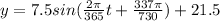
b)
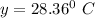`y = 28.36^0 \ C` ( to two decimal places)

Explanation:

This data can be represented by the sinusoidal function of the form :

`\mathbf{y = A sin (Bt -C)+D}`

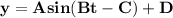
where A = amplitude and which can be determined via the formula:

`A = (largest \ temperature - lowest \ temperature)/(2)`

`A = (29-14)/(2)`

`A = (15)/(2)`

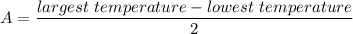
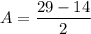
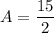
A = 7.5° C

where B = the frequency;

Since the data covers a period of 3 days ; then
`(2 \pi)/(B ) =365`

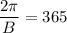
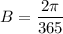`B = (2 \pi)/(365)` ( where 365 is the time period )

The vertical shift is found by the equation D;

D =
`(largest \ temperature + lowest \ temperature)/(2)`

D =
`(29+14)/(2)`

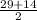
D = 21.5

Replacing the values of A ; B and D into the above sinusoidal function; we have :

`y = 7.5 sin ((2 \pi)/(365)t -C) + 21.5`

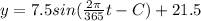
From the question; when it is 7th of the year ( i.e January 7);

t = 7 and the temperature (y) = 29° C

replacing that too into the above equation; we have:

`29= 7.5 sin ((2 \pi)/(365)*7 -C) + 21.5`

`29= 7.5 sin ((14 \pi)/(365) -C) + 21.5`

`(29-21.5)/(7.5)= sin ((14 \pi)/(365) -C)`

`1= sin ((14 \pi)/(365) -C)`

`sin^(-1)(1)= ((14 \pi)/(365) -C)`

`(\pi)/(2)= ((14 \pi)/(365) -C)`

`C= ((14 \pi)/(365) -(\pi)/(2))`

`C= ((28 \pi- 365 \pi)/(730) )`

`C= (-337 \pi)/(730)`

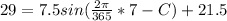
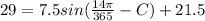
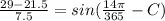
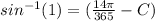
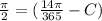
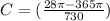
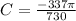
Thus; the trigonometric function is;

`y = 7.5 sin ( (2 \pi)/(365)t + (337 \pi)/(730))+ 21.5`

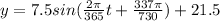
Similarly; to determine the temperature o Jan 31; i.e when t= 31 ; we have :

`y = 7.5 sin ( (2 \pi)/(365)*31+ (337 \pi)/(730))+ 21.5`

`y = 7.5 sin ( (62 \pi)/(365)+ (337 \pi)/(730))+ 21.5`

`y = 7.5 sin ( (124 \pi+ 337 \pi )/(730))+ 21.5`

`y = 7.5 sin ( (461 \pi )/(730))+ 21.5`

`y = 7.5 *( 0.915)+ 21.5`

`y = 6.8689+ 21.5`

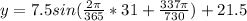
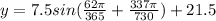
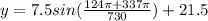
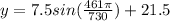
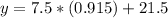
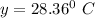`y = 28.36^0 \ C` ( to two decimal places)