Answer:
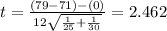
Now we can calculate the degrees of freedom given by:
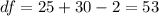
And now we can calculate the p value using the altenative hypothesis:
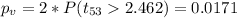
For this case the p value is lower than the significance so then we have enough evidence to reject the null hypothesis and we can conclude that the true means are different
Explanation:
We assume that the population deviation is the same for both cases
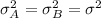
And the statistic is given by this formula:
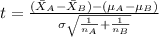
Where t follows a t distribution with
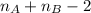 degrees of freedom
degrees of freedom
The system of hypothesis on this case are:
Null hypothesis:
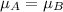
Alternative hypothesis:
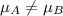
The info given is:
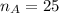 represent the sample size for group A
represent the sample size for group A
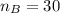 represent the sample size for group B
represent the sample size for group B
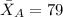 represent the sample mean for the group A
represent the sample mean for the group A
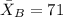 represent the sample mean for the group B
represent the sample mean for the group B
And now we can calculate the statistic:
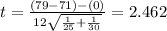
Now we can calculate the degrees of freedom given by:
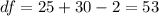
And now we can calculate the p value using the altenative hypothesis:
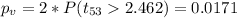
For this case the p value is lower than the significance so then we have enough evidence to reject the null hypothesis and we can conclude that the true means are different