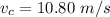Answer:
The velocity at B is
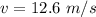
The velocity at C is
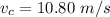
Step-by-step explanation:
From the question we are told that
The mass of the bead is

The first height is

The second height is

The initial speed of the bead is
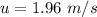
According to the law of energy conservation
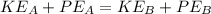
Now
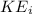 is the kinetic energy at A and it is mathematically represented as
is the kinetic energy at A and it is mathematically represented as
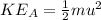
 is the potential energy at A which is mathematically represented as
is the potential energy at A which is mathematically represented as
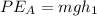
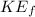 is the kinetic energy at B which is mathematically represented as
is the kinetic energy at B which is mathematically represented as
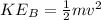
Where v is the speed of the bead at B
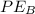 is the potential energy at B which equal to 0 because height is 0 at B
is the potential energy at B which equal to 0 because height is 0 at B
So
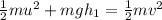
Making v the subject

substituting values
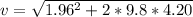
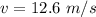
According to the law of energy conservation
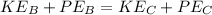
So

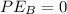
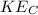 is the kinetic energy at c which is mathematically represented as
is the kinetic energy at c which is mathematically represented as
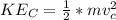
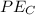 is the potential energy at C which is mathematically represented as
is the potential energy at C which is mathematically represented as
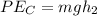
So
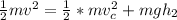
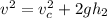
making
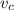 the subject
the subject